امید ریاضی

در باب اینکه امید ریاضی چی هست زیاد گفته شده و من هیچ وقت به درک عمیق از این مفهوم مهم نرسیدم و همچنان در حال تلاشم. اما دوست دارم که نتایجی که تا الان بهشون رسیدم رو باهاتون درمیان بذارم.

امید ریاضی: مقدمه

امید ریاضی در اصل میانگین وزنی است. به این صورت که هر متغیر آماری ضرب در احتمالش میشه. پس احتمال هر یک از برآمدها وزن اون برآمده. چون خیلی انتزاعی شد سعی میکنم به صورت خیلی ساده همه‌ی این‌ها رو توضیح بدم. اول از آزمایش تصادفی شروع می‌کنیم: آزمایش تصادفی یک رونده که میتونه بیشمار بار انجام بشه؛ در انتهای انجام روند، آزمایش تصادفی به ما یک نتیجه میده؛ ما نتیجه‌های مختلف آزمایش تصادفی رو می‌دونیم و اسم این نتیجه‌های مختلف رو برآمد می‌ذاریم. آزمایش تصادفی ویژگی مهمش اینه که ما تا انجامش ندیم نمی‌تونیم بگیم کدوم یکی از نتیجه‌ها/برآمدها رخ میده؛ مثل اکثر امور زندگی و جامعه. پیش‌آمد (event) با برآمد (outcome) هم معنا نیست؛ پیش‌آمد یک مجموعه متشکل از برآمدهاست. برآمد یک عضو از مجموعه‌ی تمام نتیجه‌های ممکن برای یک آزمایشه. متغیر تصادفی هم نماینده‌ی عددی برآمدهاست. یعنی هر برآمد یا نتیجه‌ی آزمایش رو به یک عدد نسبت می‌دیم؛ توی مثال‌ این‌ها براتون روشن‌تر میشه.

مثال:‌ آزمایش تصادفی، تفاوت پیش‌آمد و برآمد

اول باید یک روند پیدا کنیم که نتیجه‌اش معلوم نیست و میشه بی‌شمار بار تکرارش کرد؛ چه چیزی بهتر از پرتاب یک سکه؟ پرتاب یک سکه میتونه چه نتیجه‌هایی داشته باشه؟ شیر یا خط! این دوتا برآمدهای این آزمایش تصادفی‌ان و این آزمایش (اگر آینه اومدن رو در نظر نگیریم) هیچ حالت ممکن دیگه‌ای نداره پس برآمدهاش محدود به همین دوتان. چه پیش‌آمدهایی میشه برای این آزمایش در نظر گرفت؟ شیر، خط، شیر و خط!! پیش‌آمد شیر اومدن احتمالش نیمه، پیش‌آمد خط اومدن هم همینطور اما پیش‌آمد شیر و خط احتمالش صفره؛ چرا؟ چون ممکن نیست که ما سکه رو پرت کنیم و نتیجه هم شیر باشه هم خط! برای اینکه مبحث روشن‌تر شه آزمایش تصادفی انداختن همزمان دو سکه‌ی آبی و قرمز رو انتخاب می‌کنیم در این حالت برآمدها این‌هان: هر دو شیر بیان، سکه‌ی آبی شیر بیاد سکه‌ی قرمز خط، سکه‌ی آبی خط بیاد سکه‌ی قرمز شیر یا اینکه هر دو خط بیان! حالا من سر این شرط می‌بندم که سکه‌ی آبی شیر میاد. در این حالت من روی پیش‌آمد {هردو شیر، سکه‌ی آبی شیر و سکه‌ی قرمز خط} شرط بستم.

امید ریاضی: کاربرد در بازی‌ها

حالا میرسیم به مبحث شیرین متغیرتصادفی. فرض کنیم که یک نفر به ما یک بازی پیشنهاد می‌کنه: یک سکه پرت می‌کنیم، اگر شیر اومد شما یک هزارتومن پول میگیرید اگر خط اومد باید هزارتومن بدید. آیا بازی‌کردن یک بازی با این مشخصات عاقلانست؟ برای اینکار کافیه بتونیم متغیر‌های تصادفی رو به طور معنادار تعیین کنیم. متغیر تصادفی برآمد/نتیجه‌ی آزمایش رو به یک عدد مرتبط می‌کنه. ما در اینجا به این صورت تعیین می‌کنیم: برای شیر اومدن ۱۰۰۰ در نظر میگیریم و برای خط اومدن -۱۰۰۰:

برآمد	متغیر X	احتمال X
شیر آمدن	۰/۵	+۱۰۰۰
خط آمدن	۰/۵	-۱۰۰۰

امید ریاضی در این حالت برابره با ۱۰۰۰ در نیم به علاوه‌ی -۱۰۰۰ در نیم که میشه صفر. این یعنی چی؟ در اینجا امید ریاضی برابر با صفر به این معناست اگر این بازی رو تعداد دفعات زیادی انجام بدیم نه سودی برامون داره نه ضرری. حالا اگر بازی به نحوی باشه که مثلاً هر دفعه بازی یک کارمزد ۲۰۰ تومنی داشته باشه امید ریاضی به این صورت میشه:

برآمد	متغیر X	احتمال X
شیر آمدن	۰/۵	+۸۰۰
خط آمدن	۰/۵	-۱۲۰۰

این بار امید ریاضی برابره با منفی ۲۰۰ یعنی به طور متوسط در هر بار بازی کردن ۲۰۰ تومن می‌بازیم؛ اگر بازی رو برای مثال ۱۰۰ بار انجام بدیم درنهایت تقریباً باید ۲۰۰۰ تومن پول از جیبمون بذاریم! دفعه‌ی قبل به طور متوسط با بازی کردن نه چیزی به دست می‌اوردیم نه چیزی از دست می‌دادیم. این کاربرد امید ریاضی که الان بررسی کردیم برای بازی‌هایی مثل پوکر هم استفاده میشه!

امید ریاضی به مثابه‌ی الاکلنگ

امید ریاضی رو یا به عبارتی میانگین رو، میشه با یک مفهوم فیزیکی نشون داد: مرکز ثقل. این فقط یک مفهوم شهودیه و خیلی کاربرد ریاضی نداره. اگر یک الاکلنگ رو تصور کنیم که اجسام در انتهاش ثابت شدن برای اینکه الاکلنگ متوازن بمونه باید نصف نیرو به یک سمت الاکلنگ وارد شه و نصف دیگه‌ی نیرو به سمت دیگه. حالا که اجسام ثابت شدن فقط میشه تکیه‌گاه رو جابه‌جا کرد و تکیه‌گاه چیزی نیست جز همون میانگین یا در اینجا که وزن اجسام در دو سر الاکلنگ با هم متفاوته: امید ریاضی.

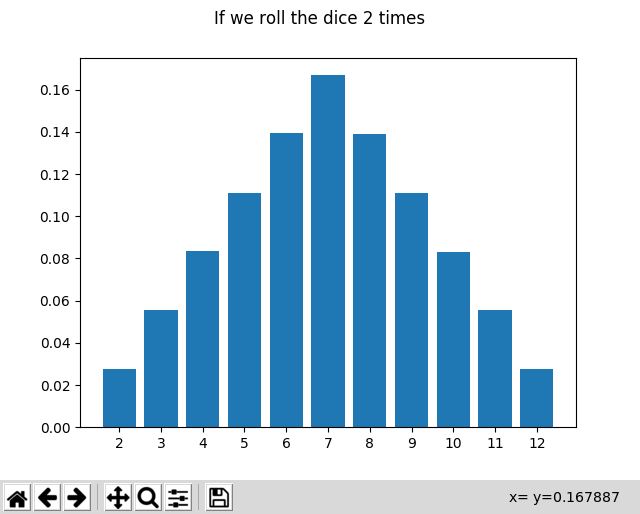
امید ریاضی: پایتون

تصویر زیر مربوط به انداختن دوتا تاسه. من برنامه رو برای انداختن K بار تاس نوشتم و توی گیت‌هابم گذاشتم. اگر مثل عکس زیر با تنظیم انداختن دوتا تاس انداختن اجراش کنید به نتیجه‌ی زیر میرسید:

به عنوان یک دانشجوی اقتصاد که از قضای روزگار این ترم «آشنایی با اقتصاد ایران» داره رفتم سبزه میدون تا از خرید و فروش دلار اطلاعات کسب کنم.

نقاطی که دلال‌های دلار در اون تجمع می‌کنن تقریبا مشخص‌اند. سبزه میدون و میدون فردوسی.

میدون فردوسی

میدون فردوسی مشابه سبزه‌میدونه با این تفاوت که توش می‌تونید فروشنده‌های خرد پیدا کنید (فروشنده‌هایی که دلار رو در مقادیر پایین می‌فروشن و می‌تونن ازتون با عابربانک پول بگیرن) و برخلاف سبزه‌میدون، دلال‌ها روبه‌روی صرافی‌ها و بانک‌ها ایستادن و دلار می‌فروشن و اما سبزه میدون…

سبزه میدون

سبزه میدون که نزدیک ناصر خسروئه و در دوقدمی ایستگاه مترو پونزده خرداد، از مراکز عمده و مشهور خرید و فروش دلاره. جوری که ممکنه بعضا در کانال‌های تلگرامی و وب‌سایت‌ها عبارت «دلار سبزه» یعنی دلاری که در سبزه میدون می‌فروشند رو ببینید.

توی سبزه‌میدون همه جور آدمی هست. یکمی که با دلال‌ها صحبت کنید یا کنارشون بایستید کلی چیز یاد می‌گیرید. مشکلی که سبزه میدون داره اینه که برای دانشجو جماعت خوب نیست. فروشنده‌ها اونجا عمده می‌فروشن. مثلا وقتی می‌گن که چقدر می‌خوای اگر بگی صدتا با اینکه اصلا به قیافت نمی‌خوره بهت می‌گن: «صدهزارتا؟» و از ثروت آدمی که روبه‌روته شگفت‌زده می‌شی! ده‌هزارتا عرفه چون که اونطور که من فهمیدم دلار رو توی بسته‌های صدتایی صددلاری جابه‌جا می‌کنن. وقتی بهشون گفتم شما خیلی پولدارید گفتن ما خیلی پولدار نیستیم، شما خیلی ضعیفید!

پیدا کردن کسی که اسکناس ۲۰ دلاری داشته باشه در حد معجزست و کسایی که اسکناس‌هایی غیر صددلاری دارن باز هم اسکناس‌هاشون رو در غالب بسته‌ می‌فروشن. مثلا صدتا یک دلاری یا در بهترین حالت ممکنه پنج‌تا بیست دلاری گیرتون بیاد؛ اونقدر تجارت براشون پر سوده و تراکنش‌ها بالا که براشون نمی‌صرفه که بهتون یک بیست‌دلاری بفروشن و حتما باید بسته‌ی صددلاری رو بخرید، که مبالغ پایینی مثل صددلار رو هم با اکراه بهتون می‌فروشن. مزیت دسته‌ای بودن پول اینه که اگر پول‌ها تقلبی باشن احتمال کشفشون بیشتره؛ می‌تونید شماره سریال پول‌ها رو نگاه کنید و اگر یکسان بود دلارها قطعا تقلبی‌ان.

مشخصا کسی پول ده‌هزاردلار رو با خودش همراه نداره و حساب‌های بانکی هم سقف ۳ میلیون جابه‌جایی در روز رو دارن برای همین ازتون «چک تضمینی» می‌خوان؛ پول نقد هم فقط و فقط در غالب تراول‌چک قبول می‌کنن. قیمت خرید با فروش فرق داره و وقتی که من اونجا بودم دلار رو ۱۵۳۰۰ میفروختن و ۱۳۰۰۰ می‌خریدن. وقتی که من رفتم با توجه به شرایط بازار فروشنده خیلی خیلی کم بود اما باز هم بستگی به دلال داشت. یک دلال وقتی کسی خواست بهش دلار بفروشه گفت سقفم پر شده، فقط فروش دارم. اما خیلی از دلال‌های دیگه فقط می‌خریدن و اصلا نمی‌فروختن.

اینکه چنین بازار پرسودی مثل بازار نزول در برخی کشورها مافیای خودش رو نداره برای من عجیبه. اطراف دلال‌ها هیچ محافظی نیست و می‌شه دلارهاشون رو زد. البته چون نزدیک بازار طلا هستن پلیس با اسلحه در چند ده‌متری‌شون ایستاده.

نحوه‌ی تعیین قیمت بهترین بخش ماجراست. قبل از ظهر همه در ساعتی مشخص وسط میدون گرد هم میان و چندنفر که پول عمده‌ای دارن شروع می‌کنن به چونه‌زنی سر قیمت. اول سر یک قیمت پایه توافق می‌کنن مثلا ۱۳ برای خرید و ۱۵ برای فروش بعد هم روی بخش خرد پول.

یکی فریاد میزنه: «۵۰ هزارتا میفروشم [پونزده و] صد» و اون شخص دیگه ممکنه قیمت بالاتر یا پایین‌تری رو داد بزنه. قیمت خرید هم به شیوه‌ی فریاد مشخص می‌شه. «۳۰ هزارتا رو [سیزده‌و]دویست می‌خرم.» ویس این قضیه رو می‌تونید توی تلگرام بشنوید یا از اینجا دانلود کنید.

دلال‌های دیگه هم که در اطراف ایستادن در نهایت با توجه به قیمت خرید قبل خودشون و قیمت موجود در بازار تصمیم میگیرن دلار رو به چه قیمتی بفروشن یا بخرن. اگر قبل از این هیاهو برید به سبزه‌میدون دلال‌ها قیمت مشخصی رو نمیگن، سه تا دلال که در فاصله‌ی سه متری از هم ایستاده بودن دلار رو به قیمت‌های مختلف می‌فروختن؛ یکی ۱۶ یکی ۱۵۵۰۰ و یکی هم ۱۵۰۰ و اونی هم که صادق بود گفت که قیمت هنوز مشخص نشده و نیم‌ساعت دیگه وسط میدون مشخص می‌شه. قدم زدن وسط این هیاهو هم کیف خاص خودش رو داره و فکر می‌کتی توی بازار سهام راه می‌ری، همه تلفن دستشونه و با اضطراب سر هم داد می‌کشن. اگر در نهایت به جیب خودتون نگاه کردید و احساس کردید که پولی که برای مترو دادید داره حروم می‌شه می‌تونید سی‌صد متر برید جلوتر و برای خودتون با قیمت دوهزار تومن آب‌طالبی بخرید! همینجاست که می‌بینید که قضیه‌ی بازار رقابت کامل نیم‌افسانه‌است و در حالی که آب‌میوه‌فروشی‌هایی که نزدیک ایستگاه متروئن و طبعا اجاره‌ی بیشتری می‌دن آب‌طالبی رو چهارهزار تومن می‌فروشن و مغازه‌های دورتر سه‌هزار و مغازه‌های دورتر دوهزار تومن. بعد هم شاد و خندون از کیفی که کردید سبزه میدون رو به مقصد خونتون ترک کنید و به خودتون قول بدید که هیچ‌وقت هوس دلار خریدن نکنید.

من اغلب می‌ترسم که پست‌های کم‌حجم بذارم و انصافا فرق میکروبلاگینگ و وبلاگ‌نویسی هم در همینه اما همین الان پست آقامون منکیو رو دیدم که یک خطه:

«حالا دیگه عاشق پمپئو شدم؛ بعد این ماجرا چطور می‌تونم عاشقش نباشم؟»

من هم این بدعت رو می‌پذیرم و گاه گاه پست‌های کوتاه کوتاه می‌ذارم.

چند روز پیش یکی از دوستان یک وبسایت بهم معرفی کرد که هنوز درگیرشم. این بازی به شما یک دروازه‌ی منطقی می‌ده:‌ نند. و شما مرحله به مرحله شروع می‌کنید به ساختن اجزای مختلف کامپیوتر، از دروازهای منطقی دیگه شروع می‌شه به RAM می‌رسه و به ساخت CPU ختم می‌شه! و جذاب تر از همه اینکه توی دنیای واقعی هم می‌تونید دستگاه رو بسازید و اگر هم نساختید با ساز و کار کامپیوتر آشنا می‌شید، به درک عمیقی از باینری می‌رسید و یکبار برای همیشه می‌فهمید زبان کامپیوتر صفر و یکه یعنی چه. موقع ساخت دروازه‌ی OR زمان بگیرید ببینید چقدر طول میکشه! در مراحل اولیه جزو سخت‌هاست :) nandgame.com

در اوایل دهه‌ی ۱۹۹۰ که محصولات فرهنگی آمریکایی در اروپا مخاطب پیدا کرده بودند فیلم‌هایی مثل «تنها در خانه» که اسم شخصیت اصلیشون کوین بود و کوین‌های بازیگر بخشی از جمعیت آلمان رو سوق دادند به سمت اینکه اسم بچه‌هاشون رو از بین اسامی انگلیسی انتخاب کنن.

این جمعیت کدوم جمعیت بود؟ طبقه‌ی ضیف. حالا ما با خیل عظیمی کوین مواجه بودیم که اکثرا از طبقه‌ی مشترکی می‌اومدن. معلم‌ها توی مدرسه کوین‌ها رو به چشم تبعیض می‌دیدن و وقتی که کوین‌ها بزرگ شدن توی سایت‌های دوست‌یابی هیچ‌کس روی اسمشون کلیک نمی‌کرد. این تاثیر یک اسم اشتباه بر شخصه.

کتاب معروف فریکونومیکس یک بخش داره که توش تاثیر اسم رو بر زندگی بررسی می‌کنه. اینکه بعضی اسم‌ها یک شخص سیاه‌پوست رو در ذهن تداعی می‌کنه و اسم بعضی‌ها یک شخص سفیدپوست رو؛ و این باعث تشدید(؟) تبعیض میشه.

وقتی که این مطلب رو به یکی از دوستانم که اهل ژاپنه نشون دادم این نکته رو اضافه کرد که چون ژاپنی‌ها و چینی‌ها اسامی‌شون رو با واژه‌نگاشت‌های عریض و طویل که بهشون می‌گن کانجی می‌نویسن و توی امتحان‌ها و تست‌ها هم لازمه که اسم شخص بالای برگه باشه، از انتخاب اسامی با نوشتار سخت پرهیز میشه تا وقت دانش‌آموز گرفته نشه!

علی‌ای‌حال حواسمون رو جمع کنیم که توی دام مد نیفتیم. مثلا بعد پخش فیلم مختارنامه اسم کیان ناگهان در لیست ۵۰ نام پسر فراوان در ایران ظاهر شد. یا اینکه سعی نکنید زرنگ‌بازی دربیارید و اسامی بین‌المللی انتخاب کنید، به این توجه کنید که احتمالا خیلی از افراد دیگه هم به ذهنشون رسیده که اسم بچه‌هاشون رو بذارن ماریا یا سایر اسامی که بین ایران و غرب مشترکه؛ و احتمالا اون‌ها هم پس‌زمینه‌ی مشابه شما رو دارن.

ترجیحا هم اسم‌هایی بذاریم که بیشتر از دو هجا نداشته باشه تا دوستای بچه‌هامون و خودمون مجبور نشی اسم بچه رو مخفف کنیم.

اسم بچه رو درست انتخاب کنیم!